Constraining Markowitz Portfolio Theory in Python

In real life, this theory is never used ‘as-is’, because the solutions are often impractical to implement due to the conditions imposed by regulation and trading institutions. Markowitz’s theory solutions have shown to be quite unstable too, so constraining the set of solutions usually improves the stability of this theory.

In this project, I analyze some of the most used constraints when applying Markowitz’s Portfolio Theory using Python. Most of the constraints implemented in this project are linear, so they can be applied using a Quadratic Programming Solver, but there is also the implementation of a non-linear constraint usually known as the cardinality constraint that consists in restricting the number of assets in the final portfolio.

Below I present some of the optimal frontiers found using different constraints:

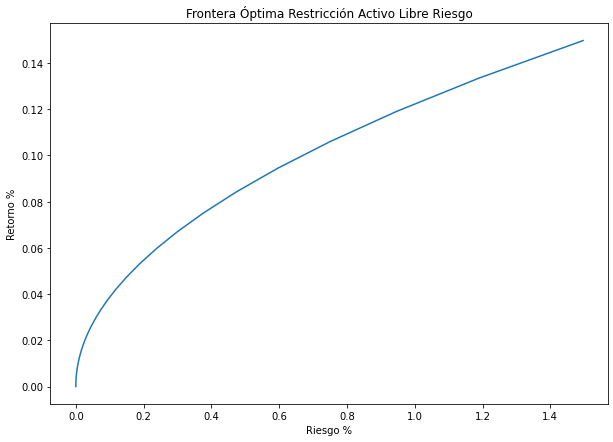
Efficient frontier considering a risk-free asset

Here the efficient frontier considers the presence of a risk-free asset in the portfolio. This addition can sometimes significantly alter the efficient frontier.

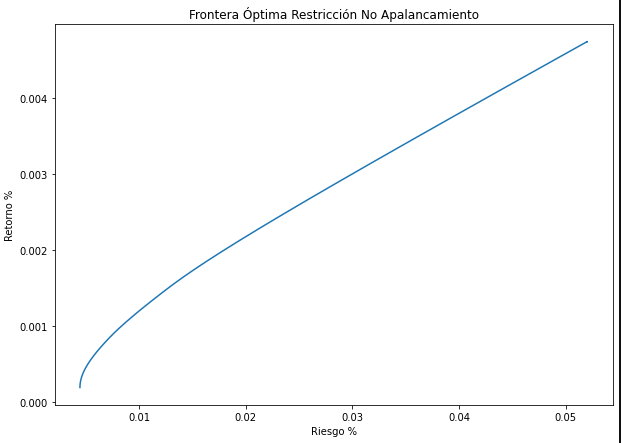
No leverage constraint

Under this constraint, Markowitz’s theory cannot yield solutions that use leverage. This constraint has an impact on riskier portfolios.

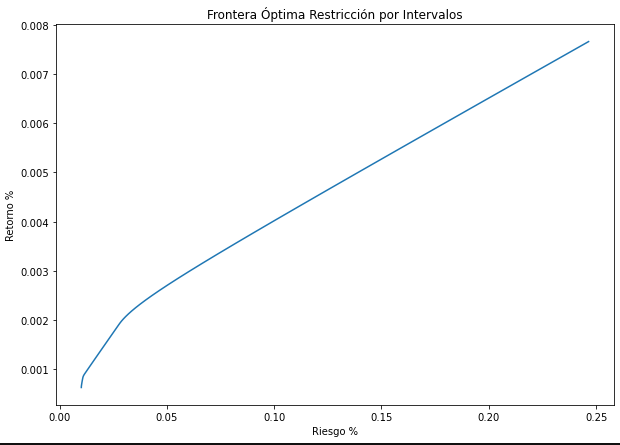
Constraining the weight of specific assets

Under this constraint, one can specify a bottom or/and top to the weight allocation of a particular asset.

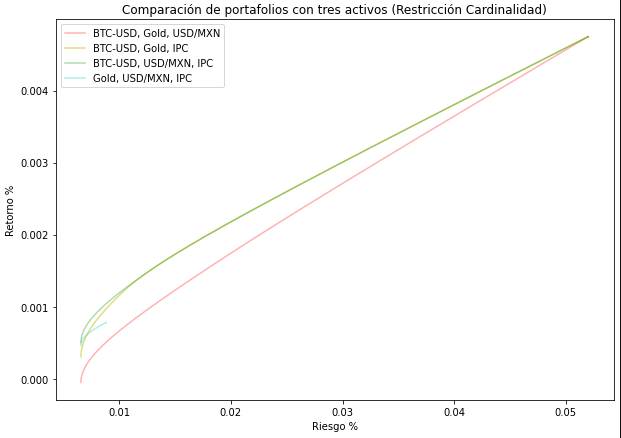
Cardinality constraint

This is a non-linear constraint that was implemented using a recursive algorithm and also a reduced set of assets. Under this constraint, portfolios of less than \(N\) assets are also considered.